Conosci Pitagora?

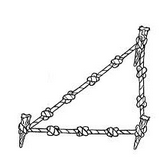
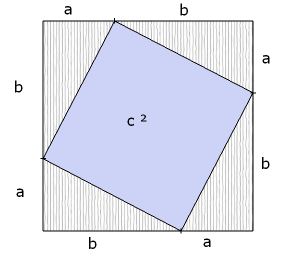
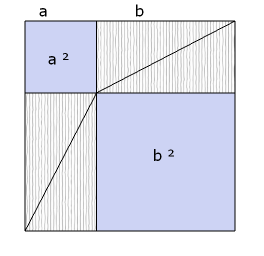
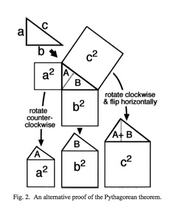
La seguente rappresentazione grafica del Teorema di Pitagora è così evidente che non traduco nemmeno il testo: le figure illustrano appieno quello che - possibilmente - fu il procedimento pratico seguito per la dimostrazione, usato in agrimensura. Geniale, semplice, efficace.

Knowing the Pythagorean Theorem

This guest post is by Sue VanHattum, who blogs at Math Mama Writes. She teaches math at Contra Costa College, a community college in the Bay Area, and is working on a book titled Playing With Math: Stories from Math Circles, Homeschoolers, and Passionate Teachers, which will be published soon.

Here’s the Pythagorean Theorem:

In a right triangle, where the lengths of the legs are given by  and , and the length of the hypotenuse is given by , we have 

Do you remember when you first learned about it? Do you remember when you first proved it?

I have no idea when or where I first saw it. It feels like something I’ve always ‘known’. I put known in quotes because in math we prove things, and I used the Pythagoeran Theorem for way too many years, as a student and as a math teacher, before I ever thought about proving it. (It’s certainly possible I worked through a proof in my high school geometry class, but my memory kind of sucks and I have no memory of it.)

It’s used in beginning algebra classes as part of terrible ‘pseudo-problems’ like this:

Two cars start from the same intersection with one traveling southbound while the other travels eastbound going 10 mph faster. If after two hours they are 10 times the square root of 24 [miles] apart, how fast was each car traveling?

After years of working through these problems with students, I finally realized I’d never shown them a proof (this seems terribly wrong to me now). I tried to prove it, and didn’t really have any idea how to get started.

This was 10 to 15 years ago, before Google became a verb, so I searched for it in a book. I eventually found it in a high school geometry textbook. Luckily it showed a visually simple proof that stuck with me. There are hundreds of proofs, many of them hard to follow.

There is something wrong with an education system that teaches us ‘facts’ like this one and knocks the desire for deep understanding out of us. Pam Sorooshian, an unschooling advocate, said in a talk to other unschooling parents:

Relax and let them develop conceptual understanding slowly, over time. Don’t encourage them to memorize anything – the problem is that once people memorize a technique or a ‘fact’, they have the feeling that they ‘know it’ and they stop questioning it or wondering about it. Learning is stunted.

She sure got my number! I thought I knew it for all those years, and it took me decades to realize that I didn’t really know it. This is especially ironic – the reason it bears Pythagoras’ name is because the Pythagoreans were the first to prove it (that we know of).

It had been used long before Pythagoras and the Greeks – most famously by the Egyptians. Egyptian ‘rope-pullers’ surveyed the land and helped build the pyramids, using a taut circle of rope with 12 equally-spaced knots to create a 3-4-5 triangle: since 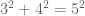 this is a right triangle, giving them the right angle that’s so important for building and surveying.

Ever since the Greeks, proof has been the basis of all mathematics. To do math without understanding why something is true really makes no sense.

Nowadays I feel that one of my main jobs as a math teacher is to get students to wonder and to question. But my own math education left me with lots of ‘knowledge’ that has nothing to do with true understanding. (I wonder what else I have yet to question…) And beginning algebra students are still using textbooks that ‘give’ the Pythagorean Theorem with no justification. No wonder my Calc II students last year didn’t know the difference between an example and a proof.

Just this morning I came across an even simpler proof of the Pythagorean Theorem than the one I have liked best over the past 10 to 15 years. I was amazed that I hadn’t seen it before. Well, perhaps I had seen it but never took it in before, not being ready to appreciate it. I’ll talk about it below.

My old favorite goes like this:

• Draw a square.
• Put a dot on one side (not at the middle).
• Put dots at the same place on each of the other 3 sides.
• Connect them.
• You now have a tilted square inside the bigger square, along with 4 triangles. At this point, you can proceed algebraically or visually.

Algebraic version:

• big square = small tilted square + 4 triangles
• 
• 
• 

Visual version:

• Move the triangles around.

• What was  is now 
• Also check out Vi Hart’s video showing a paper-folding proof (with a bit of ripping). It’s pretty similar to this one.

To me, that seemed as simple as it gets. Until I saw this:

This is an even more visual proof, although it might take a few geometric remarks to make it clear.  In any right triangle, the two acute (less than 90 degrees) angles add up to 90 degrees. Is that enough to see that the original triangle, triangle A, and triangle B are all similar? (Similar means they have exactly the same shape, though they may be different sizes.) Which makes the ‘houses with asymmetrical roofs’ also all similar. Since the big ‘house’ has an ‘attic’ equal in size to the two other ‘attics’, its ‘room’ must also be equal in area to the two other ‘rooms’. Wow! (I got this language from Alexander Bogomolny’s blog post about it, which also tells a story about young Einstein discovering this proof.

Since all three houses are similar (exact same shape, different sizes), the size of the room is some given multiple of the size of the attic. More properly, area(square) =   area(triangle), where 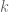 is the same for all three figures. The square attached to triangle  (whose area we will say is also ) has area , similarly for the square attached to triangle . But note that 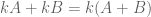 which is the area of the square attached to the triangle labeled . But , and , so  and it also equals  giving us what we sought: 

I stumbled on the article in which this appeared (The Step to Rationality, by R. N. Shepard) while trying to find an answer to a question I have about centroids. I haven’t answered my centroid question yet, but I sure was sending out some google love when I found this.

What I love about this proof is that the triangle stay central in our thoughts throughout, and the focus stays on area, which is what this is really about. It’s all about self-similarity, and that’s what makes it so beautiful.

I think that, even though this proof is simpler in terms of steps than my old favorite, it’s a bit harder to see conceptually. So I may stick with the first one when explaining to students. What do you think?